FD for Stokes equation¶
Theory¶
The finite differences method can be applied to the equations of momentum and continuity (the Stokes equation) to study the flow of a fluid.
The equation for conservation of momentum is
\begin{equation} \nabla \cdot \underline{\underline{\sigma}} + \underline{f} = \underline{0} \end{equation}
where \(\underline{\underline{\sigma}} = \eta(\nabla\underline{v}+(\nabla\underline{v})^T) - P\underline{\underline{I}}\) is the stress tensor and \(\underline{f}\) are the body forces.
This can be written, in two dimensions, separately in the x- and y-directions as
\begin{align} \eta\left(\frac{\partial^2 v_x}{\partial x^2} + \frac{\partial^2 v_x}{\partial y^2}\right) - \frac{\partial P}{\partial x} &= 0 \newline \eta\left(\frac{\partial^2 v_y}{\partial x^2} + \frac{\partial^2 v_y}{\partial y^2}\right) - \frac{\partial P}{\partial y} + \rho g &= 0 \end{align}
The continuity equation, conservation of mass, or the assumption of incompressibility, is
\begin{equation} \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} = 0 \end{equation}
These three equations are readily discretized using finite differences. Note that there are no time derivatives, but instead two spatial derivatives, in the \(x\) and \(y\) directions.
Channel flow¶
We will apply the Stokes equation to the case of orogenic channel flow. The middle and lower crust in the internal parts of large orogens may be partially molten due to the increased temperatures from crustal thickening and increased radiogenic heating. These parts of the crust might be flowing, due to the pressure gradients imposed by the mountains, towards the thinner crust surrounding the orogen.
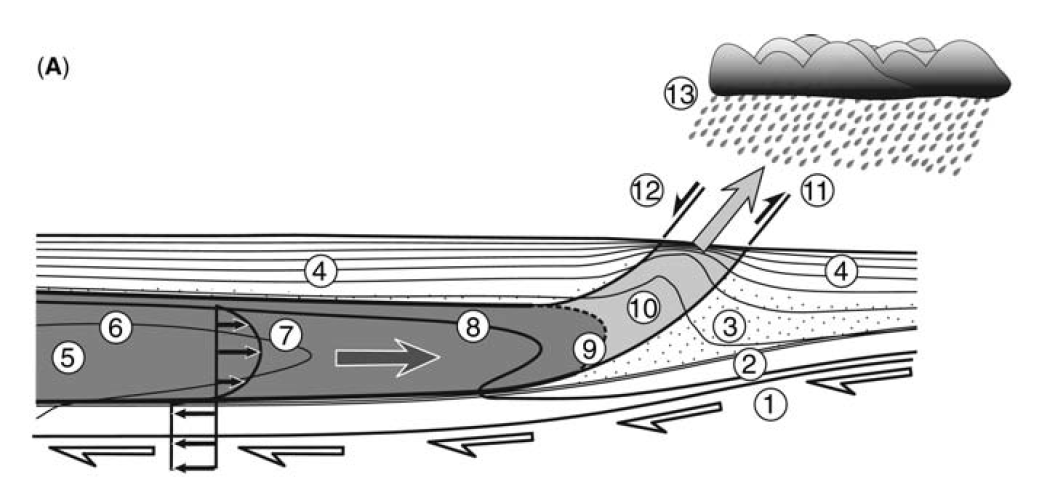
Orogenic channel flow (Godin et al. 2006). Pressure gradients drive flow to the right while the underthrusting plate imposes shearing flow towards the left.
We want to construct a one-dimensional model of this flow, by considering the horizontal velocities at different depths within the channel, and assuming that there is no vertical flow.
Since \(v_y=0\) everywhere, we can disregard the second momentum equation (y-direction). In the continuity equation \(\frac{\partial v_y}{\partial y}=0\) leading to \(\frac{\partial v_x}{\partial x}=0\). Thus, the first momentum equation becomes
\begin{equation} \eta\frac{\partial^2 v_x}{\partial y^2} - \frac{\partial P}{\partial x} = 0 \end{equation}
The value of the pressure gradient can be calculated based on the estimated lithostatic pressure difference between the channel under thick orogenic crust and the surrounding region: If we consider the extra topography by the mountain range to be \(h=4000~\mathrm{m}\), and their horizontal extent to be \(d=500~\mathrm{km}\), we get
\begin{equation} \frac{\partial P}{\partial x}\approx \frac{h \rho g}{d} = 219~\mathrm{Pa~m^{-1}} \end{equation}
The second derivative of the velocity in respect to \(y\) can be discretized using central difference, leading to: ???
Exercise - Finite difference channel flow¶
Discretize the second velocity derivative and write the whole momentum equation in the \(x\) direction
Sketch a grid with five grid points. Mark the surface and bottom grid points that will be assigned a velocity value by the boundary conditions
Looking at the figure above, what kind of boundary conditions are needed?
How would you use your discretized equation to calculate \(v_1\), the first velocity value after the uppermost grid point?
