This page was generated from source/notebooks/day-4/clusters.ipynb. Interactive online version: Binder badge

Cluster computing

Performance of geodynamic models

For example, typical 2D thermomechanical geodynamic model:

  • Dimensions 1000 km x 1000 km
  • Resolution 1 km
    • 1 000 000 grid points
    • Max. time step (diffusion limit) 16 kyrs
  • Four unknowns (\(v_x\), \(v_y\), \(P\), \(T\))
  • Four equations per grid point
  • Discretized versions of the equations: About 20 operations (+-*/) per equation
    • 80 000 000 operations (80 MFLOPS = \(80\times10^6\) FLOPS) per step
  • Modern PC processors can do about 10-100 GFLOPS (GFLOP = \(10^9\) FLOPS)
    • Processor could do 1000 steps per second
    • E.g. 50 Myrs / 16 kyrs/step = 3200 steps
    • Model run time 3.2 secs
  • BUT: Memory access time (random) approx. 50 ns
    • Each operation needs to fetch at least one number from memory
    • Worst case: random location. \(80\times10^6\times50\times10^{-9}~s=4.0~s\) per step
    • Total runtime (“wall clock time”) \(\approx 4~\mathrm{s/step}\times3200~\mathrm{steps}=3.5~\mathrm{hours}\)
  • Also, a lot of other “book keeping” during the model calculations

Do

  • Make a similar runtime estimation for a 3D model with same resolution
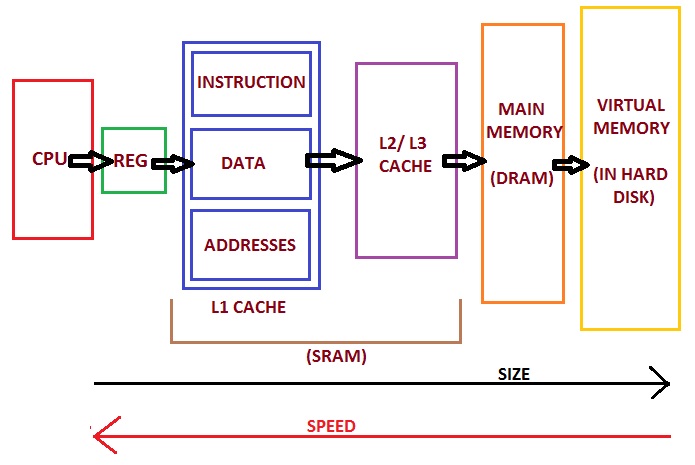
Memory hierarchy

Memory hierarchy

Memory hierarchy of modern PC (https://allthingsvlsi.wordpress.com)

The cure: Split the job among multiple processors.

  • Each will have less operations to do
    • Partitioning of the job:
      • Each processors will handle its own grid points, or
      • Each processors will handle itw own part in solving the coefficient matrix
  • Each will have smaller memory region to worry about (can store numbers closer to the processing unit)
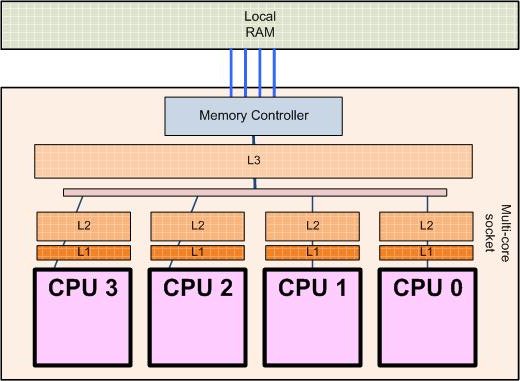
Processor architecture

Processor architecture

Processor architecture of a 4-core processor (http://sips.inesc-id.pt/~nfvr/msc_theses/msc10g/)

Modern PCs already use multiple cores (CPUs within one physical processor).

  • No speedup if the program/code used does not support multiple cores!
  • Limited (currently) to about 16 cores, typically 2-4
  • Some PC hardware allows two physical processors

More cores can be used by interconnecting multiple physical computers (nodes)

  • Needs a fast way to communicate between computers
    • Faster is better (>10 Gb/s)
  • Needs a protocol for CPUs/nodes to discuss with each other in order to distribute (partition) the work
    • One of the most common: MPI (Message Passing Interface)

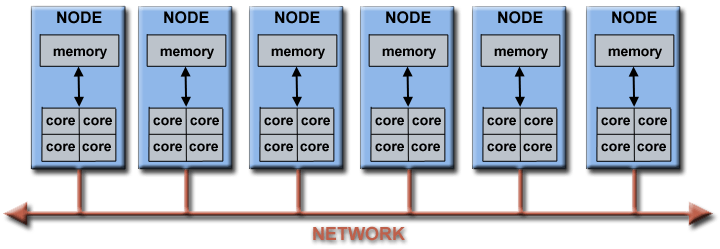
Architecture of a computing cluster

geo-hpcc cluster

  • 35 nodes, each with 2 processors, each with 8 cores = 560 cores

Performance of parallel programs

We will test the effect of running a code in parallel, using the geo-hpcc cluster.

  1. Login to the cluster using instructions at https://introgm.github.io/2018/instructions/cluster.html

  2. Type

    $ cd mpi
$ srun -n 64 python mpi.py

  3. To see and edit the Python code

    $ nano mpi.py

Do

  • Run the mpi.py script with different number of cores (modify the number after -n, try values between 1-256 cores). Keep record of core count and time elapsed. Use Excel/LibreOffice/Python to plot number of processors versus elapsed time. What kind of plot would you expect to see? What do you actually see?
  • Try plotting 2-base logarithm of time vs 2-base logarithm of number of cores used.
  • Try commands squeue and sinfo to see the job queue and the status of different nodes

Parallel performance results

You can find the results of the parallel performance exercise in the exercise summary notebook.