This page was generated from source/notebooks/day-2/fdbasics.ipynb. Interactive online version:

import numpy as np
import matplotlib.pyplot as plt

Introduction to finite differences

The method of finite differences is used, as the name suggests, to transform infinitesimally small differences of variables in differential equations to small but finite differences, thus enabling solution of these equations by means of numerical calculations in a computer. This might be necessary if the equations at hand are too complicated to be solved analytically, or if the geometry of the problem setup is too complex.

The starting point for the finite differences method is the definition of a derivative:

\[\frac{\mathrm{d}f}{\mathrm{d}x}\Big\rvert_{x=x_0} = \lim_{\Delta x \rightarrow 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{f(x_0) - f(x_0 - \Delta x)}{\Delta x}\]

However, computers can only handle numbers of finite value, not infinitesimally small values such as \(\Delta x\) at the limit used in the definition. Thus, the derivative is approximated by dropping out the limit:

\[\frac{\mathrm{d}f}{\mathrm{d}x}\Big\rvert_{x=x_0} \approx \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} \approx \frac{f(x_0) - f(x_0 - \Delta x)}{\Delta x}\]

where \(\Delta x\) is sufficiently small. If we could choose arbitrary small values of \(\Delta x\), we would reach the exact value of the derivative, but in reality we are always limited by the numerical accuracy of the computers.

n = 1
while (1 + 2**(-n) != 1):
    n = n + 1
print(n)

53

The first approximation above is called the forward difference, second the backward difference. One can define also the central difference approximation:

\[\frac{\mathrm{d}f}{\mathrm{d}x}\Big\rvert_{x=x_0} \approx \frac{ f(x_0 + \Delta x) - f(x_0 - \Delta x)}{2\Delta x}\]

Other approximations exist, too.

Taylor series approach; accuracy

Taylor’s Theorem states that function \(f\) can be presented with following series in the vicinity of \(a\):

\[f(x) = f(a) + \frac{df}{dx}\frac{(x-a)}{1!} + \frac{d^2f}{dx^2}\frac{(x-a)^2}{2!} + \frac{d^3f}{dx^3}\frac{(x-a)^3}{3!} + \ldots\]

Finite differences approximation is based on truncating the series, typically after the second term, leading to

\[\frac{f(x) - f(a)}{x-a} = \frac{df}{dx} + \mathcal{O}((x-a)^2)\]

\(\mathcal{O}\) represents the truncation error, and shows that if \(x-a\) (i.e. \(\Delta x\)) is halved, the error is dropped to one-fourth. This applies to central difference. Forward and backward differences are first-order accurate.

Approximating derivatives

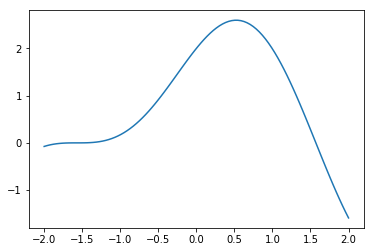
Let’s define a known function \(f(x)=\sin(2x)+2\cos(x)\) and plot it on range \(x=[-2,2]\):

def f(x):
    return np.sin(2*x) + 2*np.cos(x)

x = np.linspace(-2,2,100)

plt.plot(x, f(x))
plt.show()

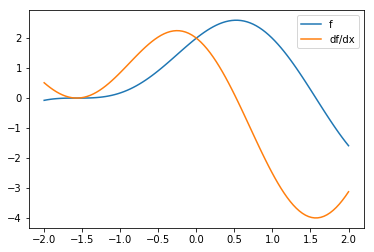
From maths we know that \(\frac{df}{dx} = 2\cos(2x) - 2\sin(x)\). Let’s define this as a python function and plot it, together with \(f\).

Do

• Define function dfdx that returns the analytically calculated derivative of \(f\)

# TODO: Define function `dfdx` here

x = np.linspace(-2,2,100)

plt.plot(x, f(x), label='f')
plt.plot(x, dfdx(x), label='df/dx')
plt.legend()
plt.show()

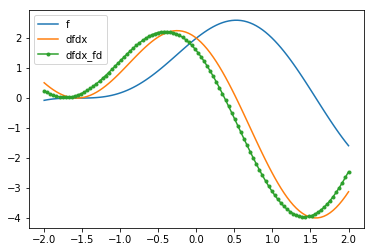
To calculate \(\frac{df}{dx}\) numerically, using finite differences, we can define a function that computes the derivative of a given function \(g\) at given position \(x_0\), using step size \(dx\).

def dfdx_fd(g, x0, dx):
    return (g(x0+dx)-g(x0))/dx

Let’s plot this on top of the analytical solution.

plt.plot(x, f(x), label='f')
plt.plot(x, dfdx(x), label='dfdx')
plt.plot(x, dfdx_fd(f, x, 0.3), '.-', label='dfdx_fd')
plt.legend()
plt.show()

Do

• Vary the third parameter dx of the last plot. Change it from 0.3 to larger and smaller values. What happens?
• Modify the definition of dfdx_fd to a) backward difference, b) central difference form. How does the derivative approximation change?

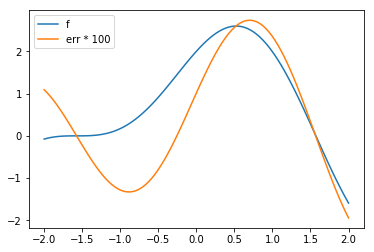
Calculating the error

def f(x):
    return np.sin(2*x) + 2*np.cos(x)

def dfdx(x):
    return 2*np.cos(2*x) - 2*np.sin(x)

def dfdx_fd(g, x0, dx):
    return (g(x0+dx)-g(x0))/dx

def err(x):
    return dfdx(x) - dfdx_fd(f, x, 0.01)

plt.plot(x, f(x), label='f')
plt.plot(x, 100*err(x), label='err * 100')
plt.legend()
plt.show()

Do

• Compare error to the function itself. When is the error (its absolute value) largest?
• Choose another function \(f\) and modify definitions of f and its analytically solved derivative dfdx above accordingly. What kind of function gives the smallest error?
• Modify dfdx_fd and implement backward or central difference approximation. How does the error change?

Applying finite differences to a physical problem

If we know the analytical form of \(f\), there is often little interest in approximating its derivative numerically. Instead, derivative approximations are used indirectly to approximate the values of \(f\) itself. Let’s see how this works in a simple example of a falling sphere.

Consider a solid sphere in a viscous fluid, with \(\rho_\mathrm{sphere} > \rho_\mathrm{fluid}\). The gravity pulls the sphere downwards, causing a buoyancy force \(F_\mathrm{b} = V\Delta\rho g = V (\rho_\mathrm{sphere} - \rho_\mathrm{fluid}) g\). The viscous fluids resists the movement of the sphere downwards. The drag caused is given by the Stokes’s law, \(F_\mathrm{d} = -6\pi\eta R v\). The sum of forces acting on the ball is then \(\sum F = m_\mathrm{sphere} a = V\rho_\mathrm{sphere} a = F_\mathrm{d} + F_\mathrm{b} = -6\pi\eta R v + V (\rho_\mathrm{sphere} - \rho_\mathrm{fluid}) g\).

Simplifying, and noting that \(V = \frac{4}{3}\pi R^3\) and acceleration \(a=\frac{dv}{dt}\), gives

\[\frac{dv}{dt} = -\frac{9 \eta v}{\rho_\mathrm{sphere} 2 R^2} + \frac{(\rho_\mathrm{sphere} - \rho_\mathrm{fluid}) g}{\rho_\mathrm{sphere}}\]

When the sphere has reached its terminal velocity, acceleration is zero, so \(dv/dt = 0 \Rightarrow v = \frac{2}{9}\frac{\Delta \rho R^2 g}{\eta}\)

def vel_term_stokes(rhosphere, rhofluid, radius, viscosity):
    return (2.0/9.0)*(rhosphere-rhofluid)*radius*radius*9.81 / viscosity

A marble with radius of 2 cm in honey:

vel_term_stokes(2800, 1300, 0.02, 250)

0.0052320000000000005

We could solve the problem by integrating both sides of the expression for acceleration. However, as an example, we will solve this numerically. To apply finite differences, we replace all derivatives with their finite approximations at time \(t_0\). In this case,

\[\frac{dv}{dt}\Big\rvert_{t=t_0} \approx \frac{v(t_0+\Delta t) - v(t_0)}{\Delta t}\]

Inserting this into the previous formula gives \(\frac{v(t_0+\Delta t) - v(t_0)}{\Delta t} = -\frac{9 \eta v(t_0)}{\rho_\mathrm{sphere} 2 R^2} + \frac{(\rho_\mathrm{sphere} - \rho_\mathrm{fluid})g}{\rho_\mathrm{sphere}}\). Note that on the right hand side \(v\) has been replaced by \(v(t_0)\).

In other words, if we know velocity at some time \(t_0\) (i.e. \(v(t_0)\)), we can calculate the velocity after time \(\Delta t\) has elapsed:

\[v(t_0 + \Delta t) = \left(-\frac{9 \eta v(t_0)}{\rho_\mathrm{sphere} 2 \pi R^2} + \frac{(\rho_\mathrm{sphere} - \rho_\mathrm{fluid})g}{\rho_\mathrm{sphere}}\right) \Delta t + v(t_0)\]

Let’s write this as a python function:

def vel_next(vel_prev, dt, rhosphere, rhofluid, radius, viscosity):
    return (-9*viscosity*vel_prev / (rhosphere*2*radius*radius) + (rhosphere-rhofluid)*9.81/rhosphere)*dt + vel_prev

dt = 0.0001
v0 = 0.0
v1 = vel_next(v0, dt, 2800, 1300, 0.02, 250)
v2 = vel_next(v1, dt, 2800, 1300, 0.02, 250)
v3 = vel_next(v2, dt, 2800, 1300, 0.02, 250)
v4 = vel_next(v3, dt, 2800, 1300, 0.02, 250)
v5 = vel_next(v4, dt, 2800, 1300, 0.02, 250)
v6 = vel_next(v5, dt, 2800, 1300, 0.02, 250)
v7 = vel_next(v6, dt, 2800, 1300, 0.02, 250)
v1, v2, v3, v4, v5, v6, v7

(0.0005255357142857143,
 0.000998283242984694,
 0.0014235449708098922,
 0.0018060906768669342,
 0.002150211032985211,
 0.0024597657283326785,
 0.0027382267600849766)

We can automate the calculation of the steps:

dt = 0.0001   # time step size
v0 = 0.0      # initial condition
nt = 50      # num of tsteps to calculate

v = np.zeros(nt)   # stores calculated velocities
t = np.zeros(nt)   # stores total time in seconds

v[0] = v0
t[0] = 0.0

for it in range(1,nt):
    v[it] = vel_next(v[it-1], dt, 2800, 1300, 0.02, 250)
    t[it] = t[it-1] + dt

plt.plot(t, v, '.-')
plt.show()

print("Velocity at time ", t[-1], " s is ", v[-1])

Velocity at time  0.0049  s is  0.005202758993971469

Do

• Use the code above to investigate what happens if the ball is being dropped from an elevation just slightly above the surface of the fluid. How do you need to modify the code?
• Take the finite differences approximation of the equation and replace \(v(t_0)\) on the right hand side by \(v(t_0 + \Delta t)\). Rearrange the equation so that you have an expression for \(v(t_0 + \Delta t) = \ldots\).
• Implement a function vel_next_implicit, similar to vel_next that calculates the velocity at next time step, but uses this modified expression.
• Copy and modify the code above so that you create a storage for both velocity values calculated using vel_next and vel_next_implicit, and plot the outcome on top of each other. Vary the value of dt and see what happens.

# Implement `vel_next_implicit` here

The first approximation (vel_next) is the forward difference approximation. vel_next_implicit is the backward difference approximation. When applied to functions of time, these are also called explicit and implicit approximations.